You have a dinner party, and you hope $k$ people will be there. For the occasion, you've bought a circle of cheese that you want to cut into equal slices, one for each guest. However, you have bought Swiss cheese which has many bubbles in it. The cheese is represented as a two-dimensional circle of radius $R$ with many other circles (bubbles) strictly inside it. No bubble will touch the outer border or the center of the cheese circle.
After cutting the slices, you will remove all the crumbs; crumbs are parts that are disconnected from the center of the cheese circle, no matter how large they are.
Find if it's possible to cut the cheese into slices such that after removing the crumbs, the outer border of the cheese remains as a complete circle of radius $R$. Since you are not sure if all your friends will come, find the answer for all number of slices from $1$ to $k$. Note that the entire cheese should be divided, resulting in the required number of slices, no less or more.
Please check the picture and the notes in the following page.
Input
The first line of input contains a single integer $T$ ($1 \le T \le 16$), the number of test cases.
The first line of each test case contains three integers $n$, $R$, and $k$ ($1 \le n \le 2000$, $3 \le R \le 10^5$, $1 \le k \le 100$), the number of bubbles in the cheese, the radius of the cheese circle, and the maximum number of slices you may need.
The $i^{th}$ of the following $n$ lines will contain three integers $x_i$, $y_i$ and $r_i$, the $x$ and $y$ coordinates of the $i^{th}$ bubble and its radius, respectively.
It's guaranteed that all bubbles are strictly inside the cheese circle and no bubble will touch or cover the center of the cheese circle.
Output
For each test case, print a single line with $k$ characters, the $i^{th}$ character should be 1 if it is possible to cut the cheese into $i$ slices according to the statement, otherwise it should be 0.
It's guaranteed that the answer will not change if we increase or decrease the radius of all bubbles by $10^{-6}$.
Notes
For the first test case, it is possible to find a way to cut the cheese to any number of slices from $1$ to $9$, but not $10$. The picture below shows one way to cut the cheese into $9$ slices.
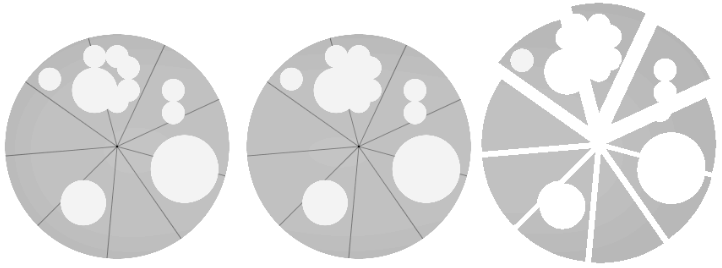
You can see the state after removing the crumbs in the middle, and to the right, we have exactly $9$ slices, and the outer part of each slice is an arc of the cheese circle.
Samples
| Input | Output |
|---|---|
2 11 10 10 1 7 1 0 8 1 1 5 1 0 4 1 5 3 1 -2 8 1 6 -2 3 5 5 1 -3 -5 2 -2 5 2 -6 6 1 1 10 17 4 -4 3 Copy
|
1111111110 11111111111000000 Copy
|