To witness secrets sealed, one must endure the harshest punishment.

The Knight wants to cross the Path of Pain. The Path of Pain is a sequence of floors and spikes. The Knight can stand on floors, but he dies if he stands on spikes. The Path of pain may look something like this:

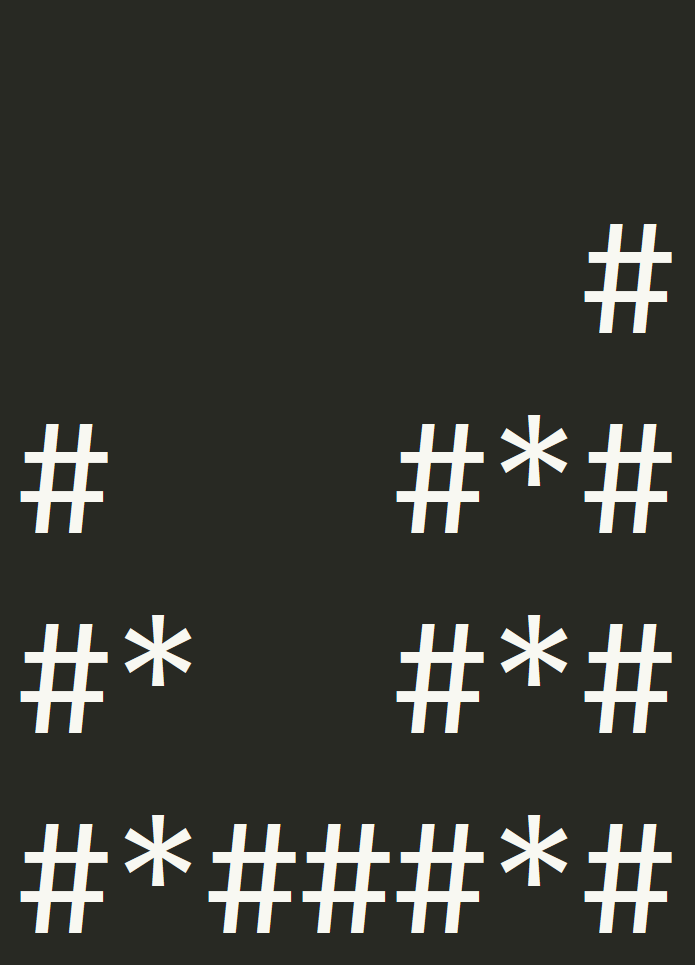
Where a $\#$ represents a floor and a $*$ represents spikes. The Knight starts on the leftmost floor and wants to end up on the rightmost floor.

The Knight has three moves:

1. Walk: move one block to the right to a floor with equal or smaller height. The Knight has to be standing on a floor to perform this move.
2. Jump: jump up to two blocks upwards. The Knight has to be standing on a floor to perform this move.
3. Dash: move up to two blocks to the right without touching the ground underneath. This move cannot be performed if there's a floor or spikes that block the way. This move can be performed in mid-air (i.e. right after the Knight performs a jump), but the Knight has to land on a floor before performing it again (i.e. The Knight cannot keep dashing continuously in mid-air without landing).

Since the Knight cannot fly, he will start falling after completing a jump, and after dashing or walking into empty space.

Given the description of the Path of Pain, determine whether or not the Knight can cross it without dying using only the moves described above.

The first line of input contains a single integer $n$, the length of the Path of Pain ($1 \leq n \leq 10^5$).

The next $n$ lines contain the description of the Path of Pain. The $i^{th}$ line contains two integers, $t_i$ and $h_i$.

$t_i$ is the type of the $i^{th}$ block. It can be either $\#$ for floor or $*$ for spikes.

$h_i$ is the height of the $i^{th}$ block ($1 \leq h_i \leq 100$).

It is guaranteed that the first and the last blocks will be floors, not spikes.

Output "YES" (without quotes) if the Knight can cross the Path of Pain, and "NO" (without quotes) if he cannot.

In the diagram below, which is the first example, a red arrow represents a dash, a blue arrow represents a jump, and a green arrow represents walking.