The Complete tournament

Time Limit: 1000ms

Memory Limit: 256MB

K - The Complete tournament

Submissions Submit

After watching naruto, Abdelaziz got obsessed with the ninja abilities and tried doing Kage bunshin no Jutsu, the cloning technique. By beginners' luck, he ended up with $N$ replicas of himself, including the original one.
It was cool at first, but now he wants to rest alone and get rid of the clones by defeating them in battles.
The battles will be boring to Abdelaziz if he defeated them sequentially one at a time, so he'll arrange tournament rounds in the following way:
All $N$ replicas are considered candidates.
Arrange the minimum number of complete tournaments possible such that every candidate is in exactly one tournament. Refer to the notes for details on complete tournaments.
The winners of the arranged tournaments are now the new candidates.
If there is $1$ candidate left, then that's the original Abdelaziz and he's done. Otherwise, go back to step 2.
Knowing some clones got eliminated by other clones, Abdelaziz wonders what fraction of the tournaments he was not in from all the tournaments done.

Input

The first line contains $T$ $(1 \le T \le 10^5)$ - the number of test cases.
Each of the next $T$ lines contains $N$ ($2\le N \le 10^{18}$) - The number of replicas including the original one.

Output

Print two integers $A$ and $B$, separated by spaces and a forward slash /, such that the fraction of the tournaments that Abdelaziz was not in is $\frac{A}{B}$. The fraction has to be in the simplest form.
If there are no tournaments that Abdelaziz was not in, print 0 / 1.

Notes

Complete tournaments are tournaments in which everyone has an equal chance of winning; i.e. the number of matches to the final match is equal for everyone.

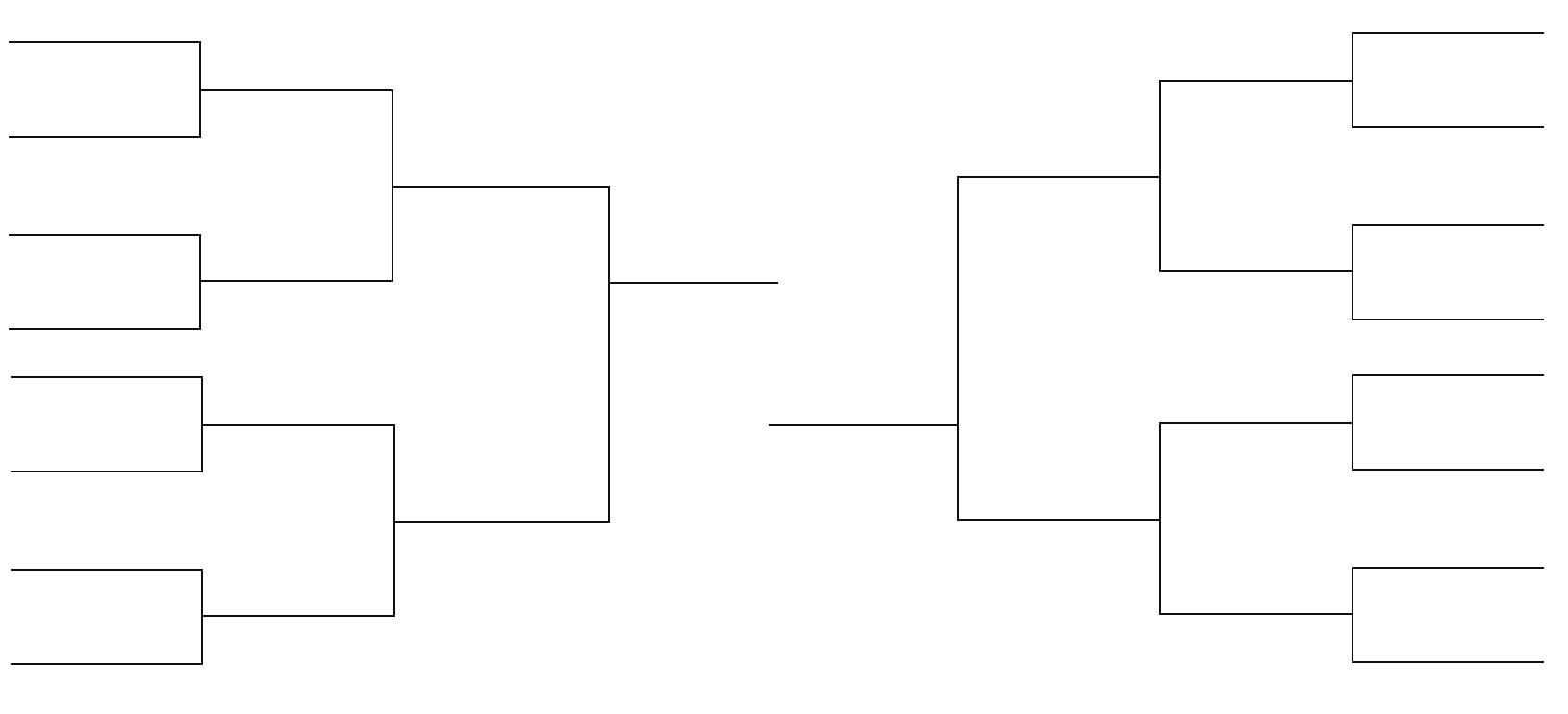
Samples

Input	Output
3 6 15 16 Copy	1 / 3 3 / 5 0 / 1 Copy

The main observation is that complete tournaments contain $2^k$ players. This helps us know that it is always best to choose the largest power of 2's to get the minimum number of tournaments; this can be inductively proven by the fact that if two tournaments are of the same power they can be merged into one larger tournament thus minimizing the total number of tournaments.
Based on that, we can just count the bits in the initial $N$ and that would give us the number of tournaments and thus the number of the candidates for the next cycle.
We keep iterating over that until we reach $1$ candidate, the original one, and here we know the total number of tournaments, call it $m$ and the number of iteration levels needed to reach that $1$, call it $l$.
Note that the original one participates in $l$ tournaments.
The answer now is $\frac{m-l}{l}$, and we can get the simplest form by dividing both over $gcd(m-1,l)$.