You are given a regular $n$-sided polygon $P$ where each side is of length $l$. You want to find the largest circle $C$ such that the polygon and the circle share the same point of center, and $\frac{A(P \times C)}{A(C)} \geq \frac{k}{10000}$. $A(C)$ is the area of the circle and $A(P \times C)$ is the area of the intersection between the circle and the polygon.
Input
The input is made up of one line containing $3$ integers $n,l,k$($3 \leq n \leq 500, 1 \le l \le 10000, 100\leq k \leq 10000)$, number of edges of the polygon, length of each edge of the polygon, and the numerator of the fraction in the statement above.
Output
Print a single number, the largest radius of the circle such that the aforementioned equality is true.
The output is considered correct if it has a relative or absolute error of at most $10^{-9}$. Formally, let your answer be $a$, and the jury's answer be $b$. Your answer is considered correct if $\frac{|a-b|}{max(1,b)} \leq 10^{-9}$.
Samples
| Input | Output |
|---|---|
5 3 8636 Copy
|
2.3704806113 Copy
|
Let's use binary search on the radius of the circle, to do that, we need to know the area of intersection for a given radius.
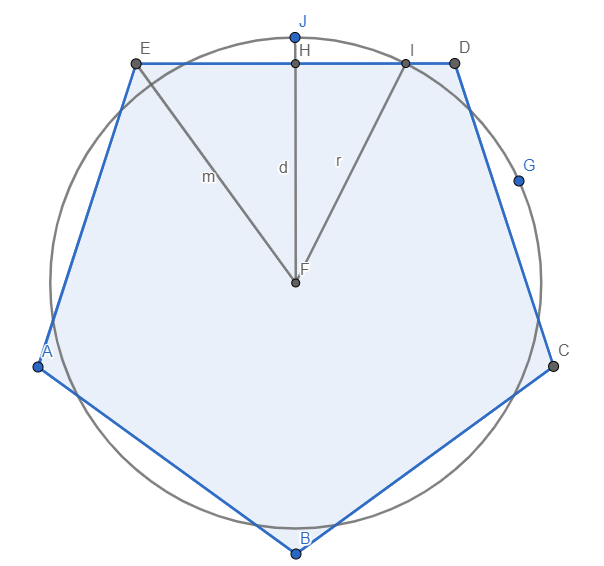
If the radius is smaller than the length of $d$ then the area of the intersection is equal to the area of the circle, if the radius is larger than the length of $m$ then the area of the intersection is equal to the area of the polygon.
Otherwise, the area of the intersection is equal to $A(C) - 2n(A(S) - A(T))$, where $S$ is the circular sector $JFI$ and $T$ is the triangle $HFI$. In order to find these values, we need to find the length of $d$, we can find it from the triangle $EFH$, we already know the length of $EH$ and the angle $EFH$($\frac {\pi} {n} $), we can get the angle $FEH$ since the angle $EHF$ is right and thus we can find the length of $d$ with sines law, also the length of $m$.
After knowing $d$ we can get the angle $HFI$ which allows us to calculate the area of the triangle T and the area of the circular sector S, thus solving the problem.