Spin the wheel

Time Limit: 4000ms

Memory Limit: 256MB

T - Spin the wheel

Submissions Submit

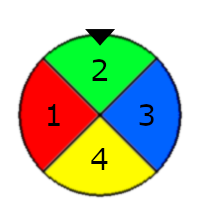
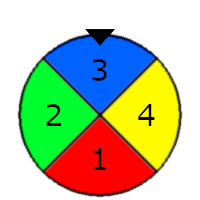
A spinner wheel is a wheel divided into $m$ sectors, sector $i$ is colored with color $i$, a wheel has a chosen color indicated by the triangle as shown below, you can spin the wheel to change the chosen color, for example the below wheel was spun one color counter-clockwise to change the chosen color from 2(green) to 3(blue). 
 
 You have $n$ spinner wheels in a circle numbered from $1$ to $n$, where wheel $i$ is adjacent to wheel $i + 1$ for all $1 \le i \lt n$ and wheel $n$ is adjacent to wheel $1$. In one operation you can select two adjacent wheels and spin one of them one color clockwise and the other one color counter-clockwise. For example, if $n=4$ and $m=5$ and the currently chosen colors are ($4,2,5,3$) then these are two possible operations you can do: 
Select the third and fourth wheel, spin the third counter-clockwise and the fourth clockwise, the circle transforms from ($4,2,5,3$) to ($4,2,1,2$).
Select the fourth and first wheel, spin the fourth clockwise and the first counter-clockwise, the circle transforms from ($4,2,5,3$) to ($5,2,5,2$).
A circle of wheels is called pretty if all wheels have the same chosen color, you're given the currently chosen color for each wheel and you can do as many operations as you like, how many different pretty circles can you make? Two pretty circles are different if their wheel's chosen color is different

Input

The first line contains two integers $n,m$($2 \le n \le 10^6, 1 \le m \le 10^{18}$), the number of wheels in the circle and the number of colors each wheel is divided into.
 
The second line contains $n$ space separated integers $c_1,c_2,...,c_n$($1 \le c_i \le m$) the currently chosen color for the $i$th wheel.

Output

Print a single number, the number of possible pretty circles you can make.

Notes

First example:
 
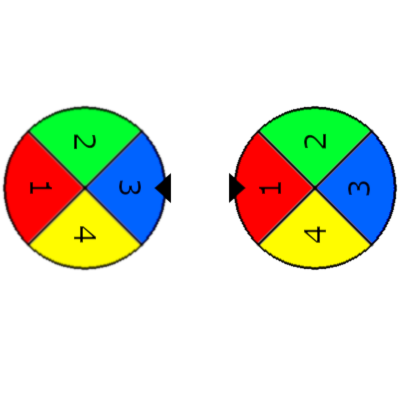
You can make two pretty circles from it, one where the chosen color is 2(green) for both wheels and another where the chosen color is 4(yellow) for both wheels.
 
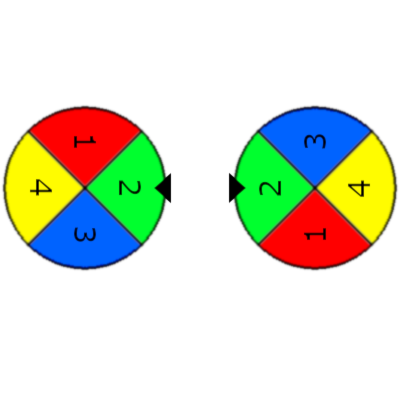
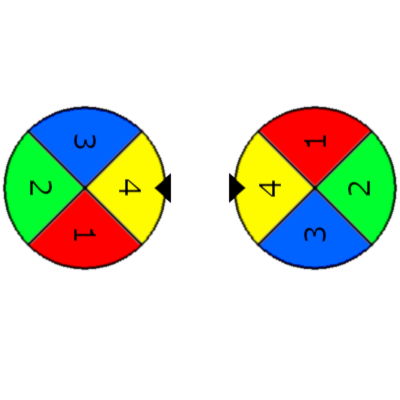
Second example:
 
No matter how many operations you do, you can't make the circle pretty.

Samples

Input	Output
2 4 1 3 Copy	2 Copy
4 4 1 2 3 4 Copy	0 Copy

For simplicity, let's assume that the colors are numbered from $0$ to $m-1$ instead of $1$ to $m$, and let's use the following example throughout the tutorial:
 
5 6
 
0 3 1 5 2  
 
Let $S$ be the sum of the currently chosen colors, for our example $S=0+3+1+5+2=11$, notice that the value $S \mod m$ doesn't change whenever you do an operation(if the reason is not clear, I recommend studying more about number theory).
 
So suppose that we want all wheels to have the color $0$, we will do operations on the first two wheels until the first one is 0, then we will do operations on the second and third wheel until the second wheel is 0, and so on until the fourth wheel is $0$, now if we do operations on the last and the first wheel we will change the value of the first wheel which we don't want, but notice that since the value of $S$ doesn't change mod $m$, if all values are known except the last one then we actually know the last value.
 
In our example, if we do operations so that the first four values are $0$, then we know that the last value will be $5$, because $5$ is the only value we can have as the last wheel that will keep $S \equiv 11 \equiv 5 \mod m$, notice that the last value can't be equal to $1$ for example, since then the summation of all values mod $m$ will be equal to $1$, but the summation has to be equal to $5$, and only putting $5$ as the last value will make the summation equal to $5$ modulo $m$.
 
So now we can do this solution: try to set the first $n-1$ wheels to every value from $0$ to $m-1$ and see if the last value will be the same as the first $n-1$ values, but that is too slow.
 
Now notice that it's only possible to make all wheels have some value $z$ if $zn \equiv S \mod m$. If that equation is true then when setting the first $n-1$ values to $z$, the last value will also be $z$, if the equation is not true, then the last value won't be equal to $z$, so the number of pretty circles is the number of $z$ values the satisfy the equation.
 
Solving the equation above requires somewhat basic knowledge of number theory, so if you're having difficulty with it, I recommend studying and understanding more about the basics of number theory, but this is a quick insight on how to solve it:
 
divide $n,S$ and $m$ by $gcd(n,S,m)$
if $gcd(n,m) \neq 1$ then no matter what the value of $z$ is the equation will never be satisfied, since $z \equiv \frac{S}{n} \mod m$
otherwise the answer is original value of $m$ divided by new value of $m$(after division).