Rahaf and Wa'el are playing with a frisbee in the City of Towers. The city consists of $n$ adjacent towers, where the height of the $i^{th}$ tower is $h_i$ meters, and the width of each tower is $1$. Rahaf is standing on top of the tower of index $r$, and Wa'el is standing on top of the tower of index $w$. For Rahaf to be able to throw the frisbee to Wa'el, there has to be a clear straight line of sight between them, i.e. a straight line (this line can be slanted at any angle) that is not blocked by a tower. Also, Wa'el has to be standing on top of one of the towers.

Rahaf has a jetpack that allows her only to fly vertically upwards. Her jetpack only contains $k$ liters of fuel, allowing her to fly a maximum of $k$ meters upwards if she wants. Wa'el, on the other hand, can climb and traverse towers easily by jumping from one tower to the adjacent ones. If it's a shorter tower then he can just jump down to it, otherwise he'll have to grab the other tower (on the same height of the one he's standing on) and climb upwards to the top of the that tower, which allows him to move to any of the other towers.

Wa'el is a lazy one, he's fine with jumping down but he doesn't want to climb up too much. Can you tell Wa'el what is the minimum total height that he has to climb so that Rahaf can throw him the frisbee? Note that Rahaf and Wa'el cannot be standing on the same tower when Rahaf wants to throw the frisbee, since that's not fun.

The first line of input consists of four integers, $n, r, w, k$ ($2 \leq n \leq 10^5, 1 \leq r, w \leq n, r \neq w, 0 \leq k \leq 10^4$), the number of towers, the position of Rahaf, the position of Wa'el, and the amount of fuel that Rahaf has in her jetpack respectively.

The second line contains $n$ space-separated integers $h$ ($0 \leq h_i \leq 10^4$), where $h_i$ indicates the height of the $i^{th}$ tower.

The output should contain a single integer $d$, the minimum total distance that Wa'el has to climb up (note that this distance does not include the distance he jumps down from a higher tower to a lower tower).

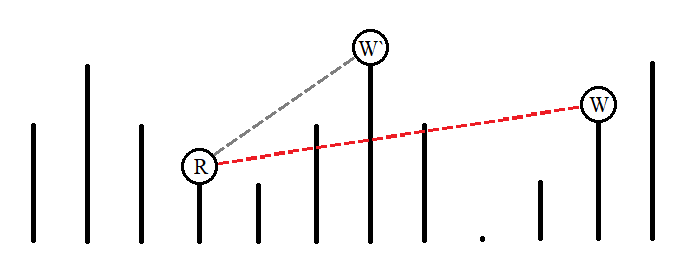
This diagram visualizes the first example. The red line shows that the line of sight between Rahaf and Wa'el is initially obstructed by a tower, while the grey line represents the direct line of sight between them after Wa'el moves to the $7^{th}$ tower.