Mirrors

Time Limit: 2000ms

Memory Limit: 256MB

Mirrors

Submissions Submit

Bob is an explorer, he wants to explore an $n \times m$ grid. in this grid there are four types of cells, an empty cell ' . ' , a blocked cell '#', a diagonal mirror '\' and another diagonal mirror '/', he is interested in exploring the empty cells of this grid as he believes there might be a buried treasure in one of them.
Unfortunately the grid is completely dark and Bob lost his flashlight, luckily you have a special type of flashlight that you can put in an empty cell, this flashlight lights the cell you put it in and also sends a ray of light in all four directions (up, down, left and right) that lights any cell it passes through, of course if the ray of light hits a mirror, it's reflected in the corresponding direction(for better understanding see notes), if the ray hits a blocked cell, the ray stops.
You need to find is the maximum number of empty cells you can light up if you place the flashlight optimally.

Input

The firs line of the input contains two ingeres $n$ and $m$($1 \le n,m \le 1000$), the number of rows and the number of columns in the grid.
The grid is given in the next $n$ lines each containing a string of length $m$.

Output

Print a single integer, the maximum number of empty cells you can light up using your special flashlight.

Notes

In the first example, it's optimal to put the flashlight in cell ($1,2$).
This is how the ray of light interacts with mirrors:

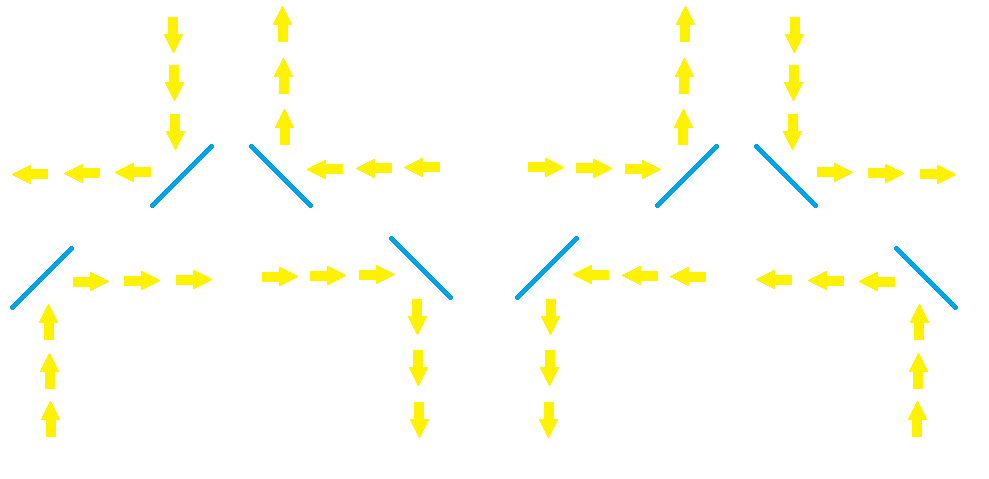
Samples

Input	Output
3 2 /. .. .. Copy	5 Copy
3 2 #. .\ #. Copy	2 Copy
3 3 /.\ .#. \./ Copy	4 Copy

A slow way to solve this problem, is to try to put the flashlight at every empty cell, and each time check how many empty cells it will light.
To improve this, let's say we put a flash light at cell $(x,y)$, look at, let's say the vertical light coming out of it, notice how if we put a flash light on any cell on that path, the light coming out from the new flashlight will always follow the same path, so once we have traced the path of a certain flashlight, we don't have to trace that path ever again.
So for every empty cell we have two possible paths for it, vertical and horizontal, if no such path was traced in this cell before with the same direction(V or H) then we should go and trace it and store for every cell on that path that we have traced it with this particular path in this particular direction. If we already traced a path in this current cell then we already have stored the information needed.
So now for every empty cell we have 2 paths that we know the length of, we can get the amount of empty cells that putting a flashlight in this cell will light up by this equation: number of cells on the first path + number of cells on the second path - number of cells that are on both paths, we can use a map of pairs to get the number of cells on both paths.
Be careful that some cells have only a single path, that is the horizontal path is the same as the vertical path, these cells should be treated separately.