Alice is standing at point ($0,0$) of the infinite Cartesian plane, she put a light bulb at that position and started moving on the plane. Alice can move in four directions(up, down, left and right), when she moves from point $a$ to an adjacent point $b$ she puts a wire on the path between them, also if there was no light bulb at point $b$, she puts one. In the end, Alice returned to point ($0,0$). It's guaranteed that she didn't move in a place that already had a wire, that is she didn't move between the same two pints more than once.
Currently all of the light bulbs Alice put are turned on, Bob wants to turn them all off , in one move he can select a light bulb that is currently turned on and turn it off, but when doing that, all adjacent light bulbs(light bulbs that are directly connected to the selected light bulb with a wire) have there state switched, that is if they were turned on they become turned off, and if they were turned off they become turned on.
Alice had moved $n$ times, you're given the description of her movements, help Bob and print a list of moves that will turn all the light bulbs off using no more than $2n$ moves or state that it's impossible to do so.
Input
The first line contains $n$($ 1 \le n \le 2 \cdot 10^5$), the number of moves Alice did.
The second line contains a string of length $n$ of the letters "LRUD" corresponding to left, right, up and down.
It's guaranteed that Alice returned to point ($0,0$) in the end.
Output
If it's possible to turn all the lights off using no more than $2n$ moves then print in the first line $m$ which is the number of moves you're going to make, then print $m$ lines each having 2 integers, the $x$ and $y$ coordinates of the light bulb you want to make a move on.
If it's not possible to turn all the lights off using no more than $2n$ moves then print "$-1$" on a single line.
Notes
The first example:
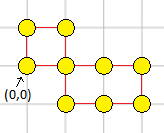
Samples
| Input | Output |
|---|---|
10 RDRRULLULD Copy
|
7 0 0 1 -1 1 0 3 0 0 0 0 1 1 0 Copy
|